
1. 먼저 a와 b를 비교하여 더 큰수를 찾는다. (a라고 가정)
2. c와 a를 비교한다. (만약 c가 a보다 크다면 크기 순서는, c > a > b 이다)
3. c가 a보다 작다면 c와 b를 비교해서 크기 순서를 결정하면 된다.
이는 a와 b중 큰 수가 b일때도 마찬가지이다
답) 3

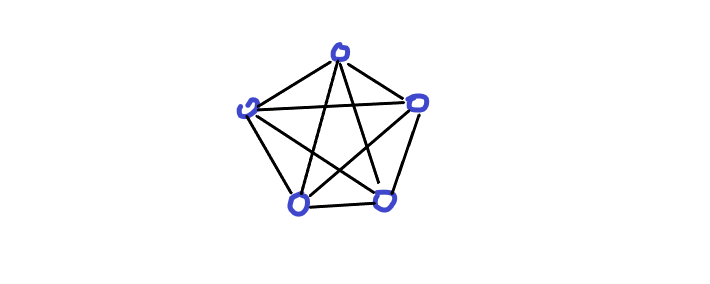
파란색 점은 사람이고 검정색 선은 친구간의 인사이다
총 합해서 10번의 인사가 진행되어야 하며, 1분에 두쌍식 인사를 한다고 해도 적어도 5분의 시간이 걸린다.
5분안에 모든 쌍이 인사를 하는 전략은 다음과 같다.

서로 평행하는 쌍끼리 인사를 진행하면, 1분에 2쌍식 5분안에 모든 쌍이 인사를 진행할 수 있다.

답) 5

두개의 서로 다른 주사위를 굴렸을 때 나올 수 있는 모든 경우의 수는 36가지이다. (6 * 6)
이렇듯 여러 상황이 독립적일 때 모든 경우의 수는, 독립적인 상황들의 경우의 수의 곱이다.
위의 과녁판 문제도 독립적인 상황이 두가지 경우의 수를 가지고 있다. (칠한다/안칠한다)
이런 상황이 5번 중첩되어 있으므로, 가능한 모든 경우의 수는 2를 5번 곱한 $2^5$이다.
답) 32

오른쪽 그림에서 물이 다 빠질 때까지 노란색 부분의 물은 빠지지 않는다. (고여있다)
따라서 노란색 부분의 제외한 칠해진 격자의 수가 물이 전부 빠지는데 걸리는 시간이다.
답) 18

201에서 300까지 세면서 박수 횟수를 세보자.
단, 쉽게 셀 수 있는 부분은 묶어서 세자
201 ~ 209 - 3번
210 ~ 219 - 3번
220 ~ 229 - 3번
230 ~ 239 - 10번
240 ~ 249 - 3번
250 ~ 259 - 3번
260 ~ 269 - 10번
270 ~ 279 - 3번
280 ~ 289 - 3번
290 ~ 299 - 10번
300 - 1번
답) 52

만나서 방향을 바꾸는 두 개미만 봤을 때, 이는 서로 무시하고 지나치는 것과 다를바가 없다
어처피 개미들끼리 딱히 구분을 하지 않기 때문에, 위의 전제로 문제를 쉽게 해결할 수 있다
가장 먼저 떨어지는 개미는 4에 서있는 개미이므로 5초 뒤 떨어진다.
가장 나중에 떨어지는 개미는 0에 서있는 개미이므로 31초 뒤 떨어진다.
답) 26

직접 그리면서 해결할 수 있는 쉬운 문제이다.
답) 5

만들 수 있는 회문의 경우의 수를 세는 문제이다.
9글자 길이의 회문을 만들때는 5번째 글자까지만 알파벳을 선택하면 된다.
그 뒤 6번째부터 9번째 글자는 앞에 결정된 알파벳에 따라 자연스럽게 결정된다. (그래야 회문이 되므로)
따라서 이 문제는 3개의 알파벳으로 만들 수 있는 5글자 단어의 경우의수를 구하는 문제와 같다.
3번 문제처럼 경우의 수를 모두 곱하면 $3^5$
답) 243

결국 직접 해봐야되는 문제이다.
40 -> 36 -> 33 -> 30 -> 27 -> 25 -> 23 -> 21 -> 19 -> 18 -> 17 -> 16 -> 15 -> 14 -> 13 -> 12 -> 11 -> 10 -> 9 -> 0
답) 19

마법의 벨을 한번씩 울리면서 규칙을 찾아보자
oo - 2
OOoo - 4
OOOOoo - 6
OOOOOOoooo - 10
OOOOOOOOOOoooooo - 16
OOOOOOOOOOOOOOOOoooooooooo - 26
...
초기값은 다르지만 피보나치 수열의 결정방식과 같다는 것을 알 수 있다.
$$F_n = F_{n-1} + F_{n-2}$$
이러한 이유는 다음과 같다.
1. n번째 어른토끼의 마리수는 n-1번째 전체토끼의 마리수와 같다.
2. n번째 어린토끼의 마리수는 n-1번째 어른토끼의 마리수와 같다.
여기서 2번의 n-1번째 어른토끼를 1번의 방식으로 재해석하면 다음과 같이 수정할 수 있다.
2. n번째 어린토끼의 마리수는 n-2번째 전체토끼의 마리수와 같다.
따라서 피보나치 수열과 같은 규칙을 가지는 것이다.
답) 9

이런 문제는 보기를 보고 만들 수 있는지 없는지를 판단하는 것이 빠르다.

7각형을 제외하고는 전부 가능하다.
여기서 볼록다각형은 내각이 180도를 넘지 않는 도형을 말한다.

위와 같은 그림은 사각형이지만, 볼록다각형은 아니다
답) 7

일단 이런 지저분한 문제를 봤을 경우 건너뛰고 뒤에 있는 문제들을 먼저 푸는 것을 추천한다
백만번째 자리를 채우는 숫자가 몇자리 수인지부터 구해보자.
1의자리 수를 전부 나열하면 총 9 * 1 = 9자리가 채워지고
10의자리 수를 전부 나열하면 총 90 * 2 = 180자리가 채워지고
100의 자리수를 전부 나열하면 총 900 * 3 = 2700자리가 채워지고
1000의 자리수를 전부 나열하면 총 9000 * 4 = 36000자리가 채워지고
10000의 자리수를 전부 나열하면 총 90000 * 5 = 250000자리가 채워진다
즉, 99999까지 나열했을 때 288889자리가 채워진다.
백만번째 자리까지 711111자리가 남았다.
100000번째 자리수가 118518개 있으면 711108자리를 채울 수 있다.
즉 100001부터 시작해서 118518번째인 218518까지 쓰면 백만번째 자리까지 세자리가 남는다.
이 세자리는 218519부터 시작하므로 백만번째 자리는 8....
인줄 알았는데 정답은 1이다.
이처럼 구하는데 오래걸리고 사소한 오류가 발생하기 쉬운 문제이므로 무조건 제치고 다른문제를 보자
아. 90000 * 5 = 250000에서 계산오류를 냈다. 다시 시작해서
10000의 자리수를 전부 나열하면 총 90000 * 5 = 450000자리가 채워진다
즉, 99999까지 나열했을 때 488889자리가 채워진다
백만번째 자리까지 511111자리가 남았다.
100000번째 자리수가 85185개 있으면 511110자리를 채울 수 있다.
즉, 100001부터 시작해서 85185번째인 185185까지 쓰면 백만번째 자리까지 한자리가 남는다
이 한자리는 185186부터 시작하므로 정답은 1이다.
답) 1
'알고리즘 > 정보올림피아드 필기 문제' 카테고리의 다른 글
| [KOI 2019] 한국정보올림피아드 1차대회 중등부 풀이 (2) | 2020.08.28 |
|---|---|
| 2014 시도예선 중고등부 문제 (2) | 2018.04.13 |
| 2013 시도예선 중고등부 문제 (0) | 2018.04.12 |
| 2012 시도예선 중고등부 문제 (0) | 2018.04.07 |
| 2011 시도예선 중고등부 문제 (0) | 2018.04.07 |