문제 링크 : https://www.acmicpc.net/problem/17608
17608번: 막대기
아래 그림처럼 높이만 다르고 (같은 높이의 막대기가 있을 수 있음) 모양이 같은 막대기를 일렬로 세운 후, 왼쪽부터 차례로 번호를 붙인다. 각 막대기의 높이는 그림에서 보인 것처럼 순서대로
www.acmicpc.net
스택을 사용하는 문제이다.
막대기가 다음과 같을 때
6 9 7 6 4 6
오른쪽에서 보이는 막대기는 다음과 같다.
6 9 7 6 4 6
막대기가 다음과 같을 때는
9 10 8 2 4 5 3 1
오른쪽에서 보이는 막대기는 다음과 같다.
9 10 8 2 4 5 3 1
막대기가 오른쪽에서 보이는지 결정하는 조건은 딱 한가지이다.
오른쪽에 자신보다 큰 막대가 없으면 오른쪽에서 보이는 막대가 된다.

두번째 예시에 있는
10의 같은 경우도 자신의 오른쪽에 10보다 크거나 같은 막대는 없다.
8 5 3 1 도 마찬가지이다.
조건을 반대로 생각하면
오른쪽에 자신보다 같거나 큰 막대가 있으면 오른쪽에서 보이지 않는다는 것이다.

그렇다면 위의 규칙을 토대로 구현을 하면 시간복잡도가 얼마나 될까
먼저 특정 막대가 오른쪽에서 보이는지 보이지 않는지 판정하기 위해서는
특정 막대 오른쪽의 막대 중 더 큰 막대가 있는지 확인해보아야 된다.

총 막대가 N개라고 하면, 최악의 경우 N개의 막대를 전부 보아야 한다.
(첫번째 막대에 대한 판정을 진행할 경우)
또한, 이 판정을 모든 막대(N개)에 대해 진행을 해야 되므로
총 시간복잡도는 $O(N^2)$이 된다.
N 제한이 100,000이므로 무조건 시간초과가 나는 방법이다..
오른쪽에 자신보다 같거나 큰 막대가 있으면 오른쪽에서 보이지 않는다는 것이다.
위 규칙의 기준을 보이는 막대가 아니라 가리는 막대로 보자
막대를 하나씩 오른쪽에 추가하면서
추가 되는 막대기가 가리는 막대들을 후보에서 지우는 것이다.

첫번째 막대부터 보자
무조건적으로 오른쪽에서 보일 수 밖에 없다.

두번째 막대기가 들어왔다
만약 왼쪽에 두번째 막대보다 작은 막대가 있었다면
그 막대는 두번째 막대에 의해 가려졌을 것이다
그러나 그런 막대는 없으므로 넘어간다

세번째 막대가 추가되었다
두번째 막대는 세번째 막대보다 작으므로 세번째 막대에 의해 가려진다
후보에서 제외해주자

네번째 막대에 의해서 첫번째랑 세번째 막대가 제외된다
후보에서 지워주자
두번째 막대는 이미 안보이는게 확정이었으므로 고려할 필요가 없다.

다섯번째, 여섯번째 막대가 추가됐다.

일곱번째 막대에 의해 여섯번째 막대가 안보이게 되었다.

여덟번째 아홉번째 막대가 추가되었다.

열번째 막대에 의해 여덟, 아홉번째 막대가 안보이게 되었다.
먼저 오른쪽에 막대를 하나씩 추가하면서
오른쪽에서 보이는 막대들 후보를 업데이트 해주었다.
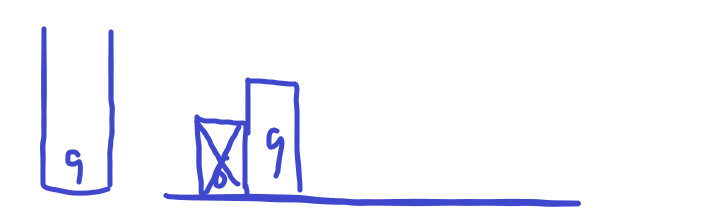
위의 그림에서는
X표가 쳐진 막대들을 제외한 막대가 후보들이었다.
후보중에서 새롭게 추가 된 막대보다 작으면 후보에서 제외해 준다
새롭게 추가 된 막대가 후보에 있는 막대들을 가리기 때문이다.
그리고 새롭게 추가 된 막대를 후보에 넣는다
가장 오른쪽에 있어서 무조건 보인다
위 과정에서 중요한 것은 후보들을 어떻게 저장할지이다
새로운 막대가 추가될 때 업데이트 되는 막대들은
후보들 중 뒤에 있는 막대들이다
즉, 늦게 들어온 막대부터 제거 대상이 되는 것이다
이를 구현하기 가장 좋은 방법은 스택을 이용하는 방법이다
6 9 7 6 4 6
처음에 봤었던 예제를 가져왔다

첫번째 막대가 들어왔다
스택에는 후보들이 저장되므로 새로 들어온 6을 넣어준다
두번째 막대인 9가 들어왔다
기존 후보에 있던 6은 9보다 작으므로 스택에서 빼준다. (후보에서 제외)
새로 들어온 9를 후보에 넣어준다

7이 새로 들어왔다
후보중에 7보다 작은 값은 없으므로 제외되는 후보는 없다
7만 추가해주자

6이 새로 들어왔다
후보중에 6보다 작은 값은 없으므로 제외되는 후보는 없다
6만 추가해주자

4도 위와 마찬가지로 후보에 추가만 해준다

새로 6이 들어와서 후보에 있던 6과 4는 안보이게 되었다
스택에서 빼고 새로 들어온 6을 추가해주자
위와 같은 과정을 거치면
스택에 남은 것이 최종 오른쪽에서 보이는 막대들이다.
#include <iostream>
#include <algorithm>
#define n_ 100005
using namespace std;
int n, m;
int arr[n_];
int stk[n_];
int main(void) {
cin >> n;
for (int i = 0; i < n; i++) {
scanf("%d", &arr[i]);
}
int top = 0;
for (int i = 0; i < n; i++) {
while (top != 0 && stk[top - 1] <= arr[i]) {
top--;
}
stk[top++] = arr[i];
}
cout << top << endl;
}'알고리즘 > PS' 카테고리의 다른 글
| [백준 10799] 쇠막대기 (0) | 2020.08.14 |
|---|---|
| [백준 9012] 괄호 (0) | 2020.08.14 |
| [백준 1085] 직사각형에서 탈출 (0) | 2020.08.04 |
| [백준 17419] 비트가 넘쳐흘러 (0) | 2020.08.03 |
| [백준 2193] 이친수 (0) | 2020.08.01 |